SilentSpiral

不定方程plus

题目

(HDU 1792) 给定互质的\(A,B\)
\(x, y\)为任意正整数
求算式 \(Ax+By\)所不能表示的最大的数
以及其所不能表示的数的个数

应该想到, 该算式有不能表示的数, 是因为\(x, y\)为正整数的约束
那么若没有这一约束, \(Ax+By\)是否可以表示任意整数呢?

证明
由裴蜀定理(也叫贝祖定理)
对于任意的\((A,B)\)总存在一对\((x,y)\)
使得 \(Ax+By=gcd(A,B)\)
由于此处\(A,B\)互质
则存在\((x_{0},y_{0})\)使得\(Ax_{0}+By_{0}=gcd(A,B)=1\)
所以\(A(kx_{0})+B(ky_{0})=k\)
所以对于任意整数 \(k\), 总存在 \((kx_{0},ky_{0})\) 满足要求

接下来该考虑如何建立约束了
注意到算式可以看作向量内积的形式
\[Ax+By=(A,B)*(x,y)\]

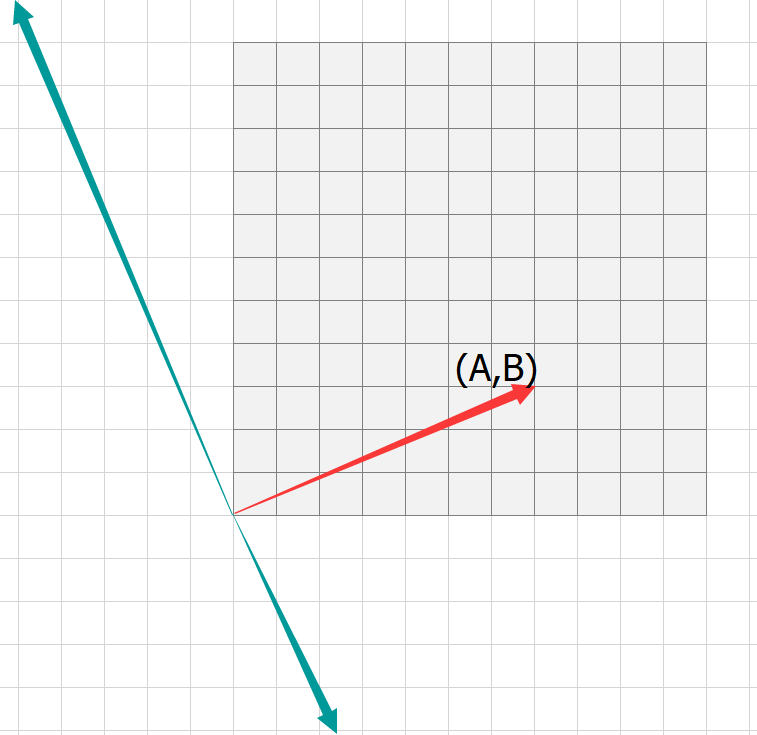
图中红线为 \((A,B)\)
蓝线以及平行于蓝线的所有直线姑且称作等积线吧
向量 \((x,y)\) 的终点落在同一等积线上的任意一点时, \(Ax+By\) 都会对应同一个值

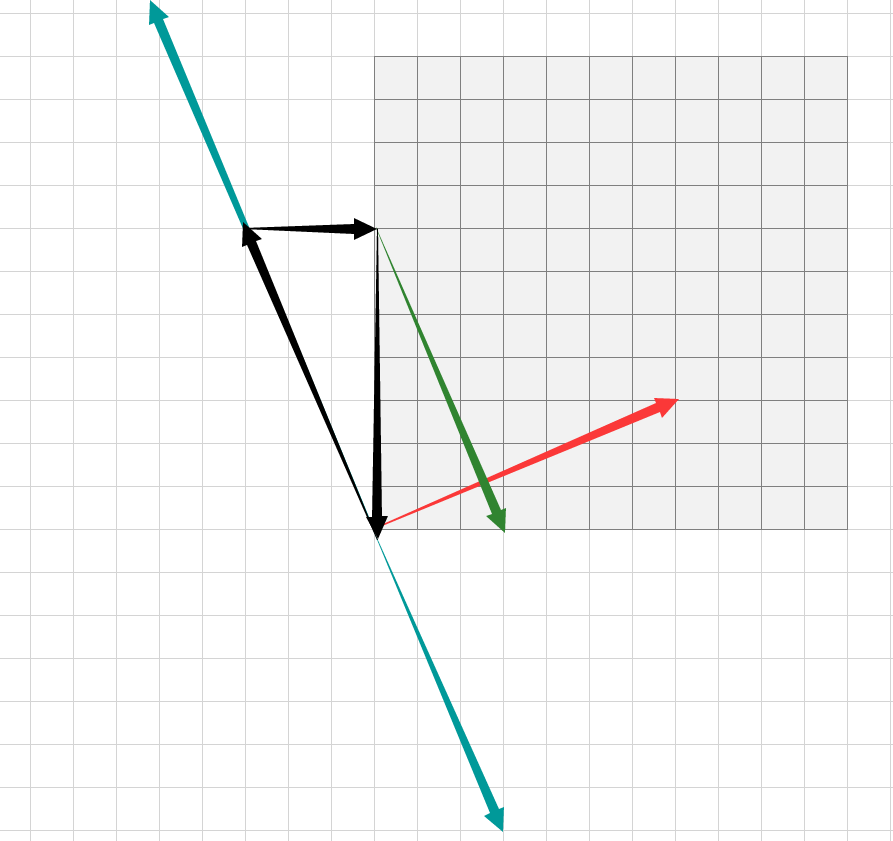
红:\((A,B)\)
蓝: 等积线
绿: 临界等积线
易知若等积线被\(xy\)正半轴所截大于\(\sqrt [] {A^{2} + B^{2}}\) ,则在第一象限一定经过某一点
等积线上两个整点的横坐标差最小必定为\(B\), 纵坐标差最小\(A\) (\(AB\)互质才有的这个性质)

绿线以外的等积线, 其对应的得数一定可以被表示出来, 因为它们在第一象限一定经过整点

所以只需要考虑蓝绿线间的所有等积线即可:

  • 每一个等积线都可以由一个整点唯一的标示出来, 易知黑色+绿色的框可以标示蓝绿线间的所有等积线
  • 对于蓝绿线间的所有等积线, 如果在第一象限没有经过整点的话,则此等积线对应的乘积不可表示
  • 绿色的框及黑色框的边界标示的等积线都可以在第一象限找到经过的整点
  • 黑框以内点标示的等积线则找不到第一象限对应的整点
  • 黑框不含边界, 共包含\(\cfrac{(A-1)(B-1)}{2}\)个整点

其中在\((A,B)\)上投影最远的点:\((-1,A-1)\)
\((A,B)*(-1,A-1)=AB-B-A\)
此即为最大不能表示的数

注: excel设置列宽为4行高26时方格为正方形

代码本体

1
2
3
4
5
6
7
8
9
10
#include<stdio.h>
int main()
{
    int A,B;
    while(scanf("%d%d",&A,&B)!=EOF)
    {
        printf("%d %d\n",A*B-A-B,(A-1)*(B-1)/2);
    }    
    return 0;
}

时间和空间复杂度都是o(1), 23333

网上找到的看不懂的证明

题意：给定A和B，A和B互质，求最大不能组合数，和不能组合数的个数。

基础知识：
$Gcd(A, B) = 1 → Lcm(A, B) = AB $ 剩余类: 把所有整数划分成m个等价类，每个等价类由相互同余的整数组成

任何数分成m个剩余类，分别为:
$mk，mk+1，mk+2，……，mk+(m-1) $
分别记为\({0\,(mod \,m)}，{1\,(mod\,m)}\)……
而n的倍数肯定分布在这m个剩余类中
因为\(Gcd(m,n)=1\)，所以每个剩余类中都有一些数是n的倍数，并且是平均分配它的旁证
可见HDOJ 1222 Wolf and Rabbit
设 \(k_{min} = min\{ k | nk ∈ \{i (\mod{m})\} \}, i ∈ [0, m)\)
则 \(nk_{min}\) 是\({i\,(mod\,m)}\)中n的最小倍数。特别的，$nm ∈ {0,(mod,m)} $
\(nkmin\)是个标志，它表明\(\{i\,(mod\,m)\}\)中\(nk_{min}\)后面所有数
即\(nk_{min} + jm\)必定都能被组合出来
那也说明最大不能组合数必定小于\(nk_{min}\)
我们开始寻找\(max\{nk_{min}\}\)
\(Lcm(m, n) = mn\)，所以很明显\((m-1)n\)是最大的
因为\((m-1)n\)是\(nk_{min}\)中的最大值，所以在剩下的\(m-1\)个剩余类中，
必定有比它小并且能被m和n组合，
这些数就是\((m-1)n -1，(m-1)n -2，……，(m-1)n -(m-1)\)
所以最大不能被组合数就是\((m-1)n -m\)

如果m和n不互素，那\(\{1\,(mod\,m)\}\)不能被m组合，同样也不能被n和m组合

我们能求出各个剩余类的nkmin之后，不能组合数的个数就是每个剩余类中小于各自nkmin的数的个数总和。
观察如下：

\(M = 5，N = 3\)
\({0(mod\,5)}：0，5，10，15……\)
\({1(mod\,5)}：1，6，11，16……\)
\({2(mod\,5)}：2，7，12，17……\)
\({3(mod\,5)}：3，8，13，18……\)
\({4(mod\,5)}：4，9，14，19……\)
红色的就是不能组合数，可以看出在剩余类中它的数目有规律
\(Total = [0+1+2] + [0+1]\)
因为m和n互质，必有一个不完全周期
整理以后，可得公式 \(Total = \cfrac{(A-1)(B-1)}{2}\)

有谁看懂了给我讲一下, 谢谢

打赏