SilentSpiral

BitRing & 欧拉回路

题目

一个环上有 2n 个位置，把他们填上0或1，使得每连续n位都能组成二进制下不互相重复的数，求出一个序列即可。

思路

譬如n=3的时候环上是8个位置

1
2
3
4
5
6
7
8
9
00101110  
001 = 1  
 010 = 2  
  101 = 5  
   011 = 3  
    111 = 7  
     110 = 6  
      100 = 4  
       000 = 0

现在需要把 0 ~ 2n-1 这些数字串起来
考察每个比特串的 前n-1位 和 后n-1位

以n=3为例

所有可能出现的组合

组合 接续关系 接续关系（Dec）
000 00 –> 00 0 –> 0
001 00 –> 01 0 –> 1
010 01 –> 10 1 –> 2
011 01 –> 11 1 –> 3
100 10 –> 00 2 –> 0
101 10 –> 01 2 –> 1
110 11 –> 10 3 –> 2
111 11 –> 11 3 –> 3

考虑右侧的组合关系，这是个有向图，每一条边代表连续n位，也就是在上面那个表里的一个箭头关系
（2指向0就是10拼上00，得100=4）

经整理，可得该图的 邻接表 ：

0 –> 0，1
1 –> 2，3
2 –> 0，1
3 –> 2，3

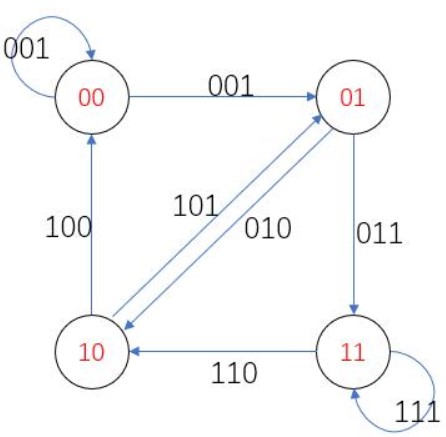
欧拉图(n=3)
欧拉图(n=3)

你需要做的是找出欧拉回路，即把它一笔画下来

那么矛盾就集中在找欧拉回路上了

Question 1：

根据这个表可否推广n=4，5，6…时的邻接表？
（当然可以）

Question 2：

这个图是否一定存在欧拉回路？
（必须的）
根据：每个节点都有两个入度两个出度，而且是联通图。

欧拉回路

欧拉回路怎么求
1、从任意一个点起，在图中寻找任意一个（不需要遍历全图的）回路，最终必定以回到这个点作为结束。
2、从图中拿掉一个回路，剩下的必定是若干个回路，且和已有回路存在公共点
3、前一条性质其实是在做减法。所以我们可以反过来用加法的形式，从一个简单回路开始不断在公共点处添加回路以拼接，直到最终生成欧拉回路。

算法

求欧拉回路的算法：
1、初始回路[0，0]，并手动修改生成了此回路后的邻接表
2、cnt=2n-2
循环（当cnt不为0）：
cnt，L，index=AddSubRing(cnt，L，index)

伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
AddSubRing(cnt，L，index)：  
    index是下标，用它扫描L  
    若扫到邻接表未全访问过的节点则更新index并从这个节点X开始生成子回路  
   从X生成回路：  
   while(节点邻接表未被全访问过)  
        if 第一个邻节点未被访问：  
              添加到回路(第一个)  
              修改visited（）  
              往后拨  
        else：  
              添加到回路(第二个)  
              修改visited（）  
              往后拨  
         cnt-=1  
     从公共点(index)合并两个回路   
    返回 cnt，L，index

存储结构

邻接表：
\((x \mod{(M>>1)})\)
\((x\mod {(M>>1)})+1\)

欧拉回路：
链表（C语言）
List（Python）

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
n=int(input())
M=(1<<(n-1))

def edge(x):
	return (x%(M>>1))<<1

def findSubRing(L,index,cnt):
	while index<=len(L):
		index+=1
		if arcs[L[index]]!=2:
			break
	tmp=L[index]
	nList=[tmp,]
	while arcs[tmp]!=2:
		q=tmp
		if arcs[tmp]==0:
			tmp=edge(tmp)  #向后拨
			nList.append(tmp)
		else:
			tmp=edge(tmp)+1
			nList.append(tmp)
		cnt-=1
		arcs[q]+=1
	NList=L[:index]+nList+L[index+1:]
	#print(nList,NList)
	return(NList,index,cnt)

arcs=[0 for _ in range(M)]
arcs[0]=1   #手动初始化第一个回路
arcs[M>>1]=1
res=[0,0]
#print([edge(x) for x in range(4)])
cnt=2*M-2
index=0
while cnt:
	res,index,cnt=findSubRing(res,index,cnt)
	#print(res)

print("\n欧拉回路:\n",res)
BitsRing=[x&1 for x in res]
print("\nBitsRing:\n","".join(["%d"%i for i in BitsRing]))
numbers=[res[(i+n-2)%(2*M)]*2+(res[(i+n-1)%(2*M)]&1)    for i in range(M*2)]
print("\nnums:\n",numbers)

哈密顿回路

上面的方案中采用了欧拉回路，以每条边表示每一个n位二进制数。遍历所有的边求出欧拉回路即可

也可以用点来表示每一个n位二进制数，以边来表示接续关系，这种情况下就需要遍历所有的点求出一个哈密顿回路。

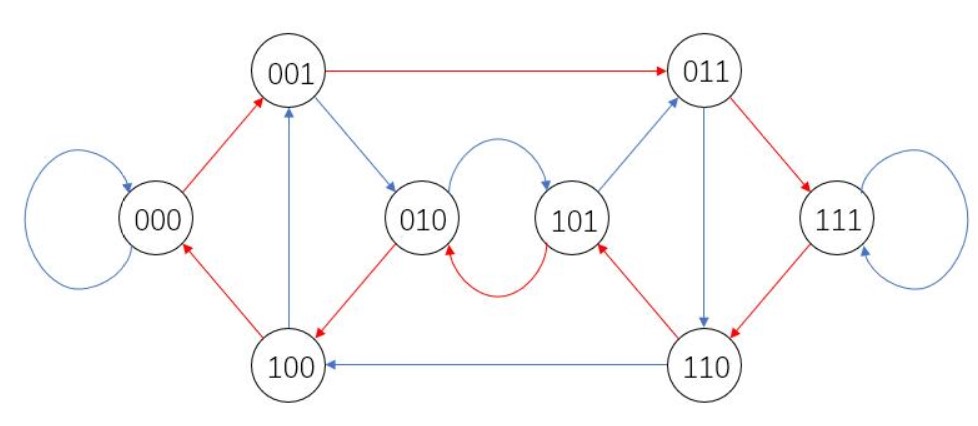
哈密顿图(n=3)
哈密顿图(n=3)

比对n=3时对应的欧拉图和哈密顿图，可以看到欧拉图的规模比较小

求解欧拉回路，上面已经实现了o(n)级别的算法。

而哈密顿回路是NP完全问题，并没有快捷的算法。

参考链接

这里有哈密顿图和欧拉图的dfs求解方法

哈密顿回路：
将每个点看成一个k位的二进制，每条边看成一个k+1位的二进制，那么一个点u向另一个点v连边当且仅当u去掉第一位后在后面加上一位能得到v，例如：001001向010010连边，边的二进制为00100010。可以发现，这个图一定存在一条哈密顿回路，那么第一问的答案显然是2k。对于第二问，因为k较小，直接暴力找哈密顿回路即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<vector>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
int vis[3000];
int ans[3000];
int k,n;
int mask;
bool dfs(int x,int dep){
    ans[dep]=x;
    vis[x]=1;
    if(dep==n)
    { return 1; }
    if(!vis[(x<<1)&mask]){
        if(dfs((x<<1)&mask,dep+1))
        { return 1; }
    }
    if(!vis[((x<<1)|1)&mask]){
        if(dfs(((x<<1)|1)&mask,dep+1))
        { return 1; }
    }
    vis[x]=0;
    return 0;
}
int main(){
    scanf("%d",&k);
    n=1<<k,mask=n-1;
    printf("%d ",n);
    vis[0]=1;
    dfs(0,1);
    for(int i=1;i<=n;i++)
    { printf("%d",(ans[i]>>(k-1))&1); }
}

欧拉回路：
如果将点看成一个k−1位的二进制，边看成一个k位二进制，那么就是求一个欧拉回路，同样暴力dfs即可。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<vector>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
int vis[3000];
int ans[3000];
int k,n;
int mask;
bool dfs(int x,int dep){
    if(dep==n)
    { return 1; }
    if(!vis[x<<1]){
        vis[x<<1]=1;
        ans[dep+1]=x<<1;
        if(dfs((x<<1)&mask,dep+1))
        { return 1; }
        vis[x<<1]=0;
    }
    if(!vis[x<<1|1]){
        vis[x<<1|1]=1;
        ans[dep+1]=x<<1|1;
        if(dfs((x<<1|1)&mask,dep+1))
        { return 1; }
        vis[x<<1|1]=0;
    }
    return 0;
}
int main(){
    scanf("%d",&k);
    n=1<<k,mask=(1<<(k-1))-1;
    printf("%d ",n);
    dfs(0,0);
    for(int i=1;i<=n;i++)
    { printf("%d",(ans[i]>>(k-1))&1); }
}

打赏